Here’s a fascinating factoid I found in Geoffrey West’s new book Scale:
An extremely simple but very powerful mathematical result for the movement of people in cities. .. Consider any location in a city. .. predicts how many people visit this location from any distance away and how often they do it. .. It states that the number of visitors should scale inversely as the square of both the distance traveled and the frequency of visitation. ..
Suppose that on average 1600 people visit the area around Park Street, Boston from four kilometers away once a month. .. only 400 people visit Park street from 8 kilometers away once a month. .. how many people visit Park street from four kilometers away but now with a greater frequency of twice a month. .. also … 400 people. (pp.347-9)
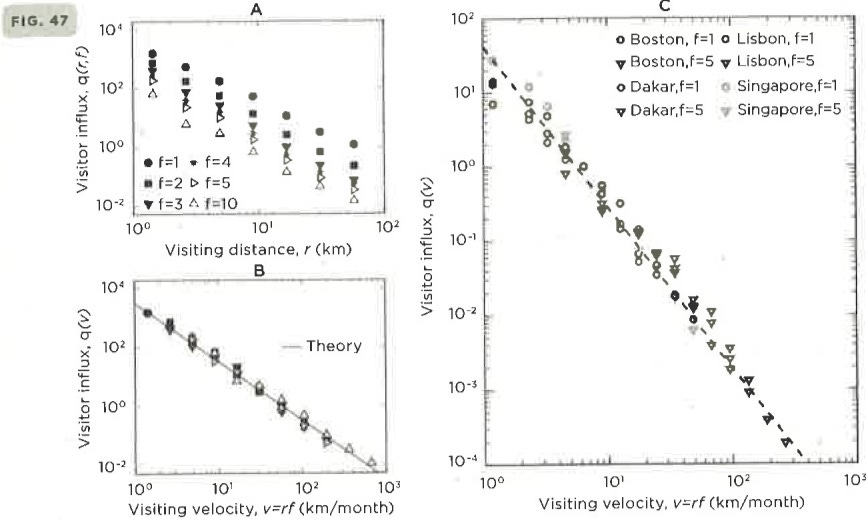
As cities are basically two-dimensional in space and one-dimensional in time, this implies that most visits to a place are by people who live nearby (not so surprising), and also by people who visit very infrequently (quite surprising). I’d love to see an urban econ model embodying this pattern. Alas West cites “Markus Schlapfer and Michael Szell”, but no publication, nor could I find one online.
The book Scale is on an important yet neglected topic: basic patterns in large systems such as organisms, ecosystems, cities, and firms. Alas West rambles, in part to avoid talking math directly, so you have to skim past many words to get to the key patterns; I bet I could have described them all in ten pages. But they are indeed important patterns.
I found myself distrusting West’s theories for explaining these patterns. He talks as if most of the patterns he discusses are well explained, mostly by papers he’s written, and he doesn’t engage or mention competing theories. But I’ve heard that many disagree with his theories. In particular, though West claims that a 3/4 power law of organism metabolism versus mass is explained by piping constraints (West offers different theories for trees and for animals with pumped blood), while researching Age of Em I learned:
Does our ability to cool cities fall inversely with city scale? Actually, no. We have good fractal pipe designs to efficiently import fluids like air or water from outside a city to near every point in that city, and to then export hot fluids from near every point to outside the city. These fractal designs require cost overheads that are only logarithmic in the total size of the city.
So if this metabolism pattern is due to piping constraints, it is because evolution never managed to find the more efficient piping designs that we humans now know.



That is if you only change is the volume of piping. But you can also change other parameters, such as pressure, to compensate. The net effect is that the cost scales as the log, and that can scale indefinitely.
If you run into a paywall, you should check Google or Google Scholar or use Libgen, the former of which would point you at https://www.researchgate.ne...